BZOJ2177 曼哈顿最小生成树 <树状数组优化建边>

Problem

曼哈顿最小生成树

Description

平面坐标系内，给定个顶点。对于顶点，与之间的距离定义为。你的任务是求出这个顶点的最小生成树。

Input

第一行一个正整数，表示定点个数。
接下来行每行两个正整数，描述一个顶点。

Output

只有一行，为最小生成树的边的距离和。

Sample Input

Sample Output

HINT

对于的数据，。

标签：树状数组 MST

Solution

裸题。

对于曼哈顿最小生成树，直接建边肯定是不行的，考虑优化建边，去掉一些一定不会在中的边。
考虑一个点，以为中心将整个图分为个部分。

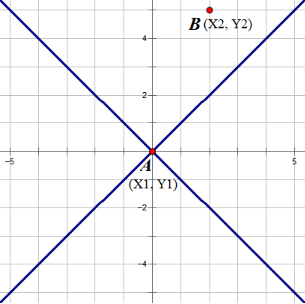
对于一个在右上角的点，一定有，若其使最小，则所有在右上角的点的曼哈顿距离都没有小。因此在右上角的所有点中，只连即可。同理在周围的八个方向中，每个方向只需连曼哈顿距离最小的点。

对于如何寻找这样的点，拿找右上角的最近点做例子：
最近的点一定使最小，即使最小。同时要满足，即满足。可以发现这就是以为第一维，为第二维做偏序，找到符合的位置中的最小值，用维护。
这样我们就可以连每个点到其右上角的最近点的边了。考虑到边可以每次都连双向，因此每个点只用枚举一半即可。这里默认向坐标比当前点大的点连边。其实是可以把每种情况都转化为右上角的。
一开始的时候，我们总共需要考虑的是下图区域中的最近点。第一次连边将中的最近点连边。

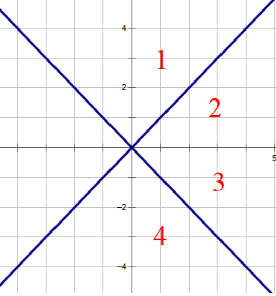
接下来将每个点的坐标互换，即关于直线对称，可以得到下图。第二次连边将中的最近点连边。

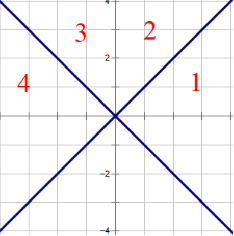
然后将每个点的坐标取反，即可得到下图。这时第三次连边将中的最近点连边。

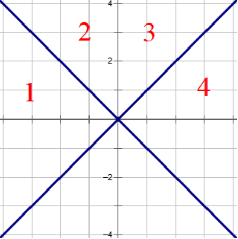
最后再次互换每个点的坐标，得到下图。第四次连边将中的最近点连边。

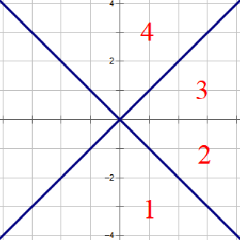
由此，我们可以不改回原值就将个方向连边。
建图后，直接跑或即可。

Code

#include <bits/stdc++.h>
#define MAX_N 100000
#define INF 4020010910LL
using namespace std;
typedef long long lnt;
template <class T> inline void read(T &x) {
    x = 0; int c = getchar(), f = 1;
    for (; !isdigit(c); c = getchar()) if (c == 45) f = -1;
    for (; isdigit(c); c = getchar()) (x *= 10) += f*(c-'0');
}
int n, cnt, fa[MAX_N+5];
lnt tr[MAX_N+5]; int mi[MAX_N+5];
struct edge {int u, v; lnt c;} E[(MAX_N<<2)+5];
struct P {int id; lnt x, y;} p[MAX_N+5], q[MAX_N+5];
bool cmpe (const edge &a, const edge &b) {return a.c < b.c;}
bool cmpp (const P &a, const P &b) {return a.x == b.x ? a.y < b.y : a.x < b.x;}
lnt dist(int u, int v) {return abs(q[u].x-q[v].x)+abs(q[u].y-q[v].y);}
void addedge(int u, int v) {E[++cnt] = (edge){u, v, dist(u, v)};}
int getf(int x) {return fa[x] == x ? x : fa[x] = getf(fa[x]);}
void modify(int pos, lnt x, int id) {
    for (; pos; pos -= pos&-pos)
        if (tr[pos] > x) tr[pos] = x, mi[pos] = id;
}
int query(int pos) {
    int ret = -1;	lnt mc = INF;
    for (; pos <= n; pos += pos&-pos)
        if (tr[pos] < mc) mc = tr[pos], ret = mi[pos];
    return ret;
}
void build() {
    int a[MAX_N+5], b[MAX_N+5], m;	sort(p+1, p+n+1, cmpp);
    for (int i = 1; i <= n; i++) a[i] = b[i] = p[i].y-p[i].x;
    sort(b+1, b+n+1), m = (int)(unique(b+1, b+n+1)-b-1);
    for (int i = 1; i <= n; i++) tr[i] = INF;
    memset(mi, -1, sizeof mi);
    for (int i = n, rk, mp; i; i--) {
        rk = (int)(lower_bound(b+1, b+m+1, a[i])-b);
        mp = query(rk); if (~mp) addedge(p[i].id, mp);
        modify(rk, p[i].x+p[i].y, p[i].id);
    }
}
lnt MST() {
    sort(E+1, E+cnt+1, cmpe); lnt ret = 0;
    for (int i = 1; i <= n; i++) fa[i] = i;
    for (int i = 1, u, v; i <= cnt; i++) {
        u = getf(E[i].u), v = getf(E[i].v);
        if (u^v) fa[u] = v, ret += E[i].c;
    }
    return ret;
}
int main() {
    read(n);
    for (int i = 1; i <= n; i++)
        p[i].id = i, read(p[i].x), read(p[i].y), q[i] = p[i];
    build(); for (int i = 1; i <= n; i++) swap(p[i].x, p[i].y);
    build(); for (int i = 1; i <= n; i++) p[i].x *= -1;
    build(); for (int i = 1; i <= n; i++) swap(p[i].x, p[i].y);
    build(); for (int i = 1; i <= n; i++) p[i].y *= -1;
    return printf("%lld\n", MST()), 0;
}